1 Introduction

Refractories are materials designed to withstand severe service conditions such as exposure to thermomechanical loads, corrosion/erosion from solids, liquids, and gases, gas diffusion, and mechanical abrasion [1]. These characteristics allow refractories to be used in high-temperature processes in a variety of sectors, including cement production, aerospace applications, and the production of iron and steel [1,2,3]. Most of the refractory consumption comes from the iron and steel-making industry, in which many pieces of equipment have refractory linings to reduce heat losses during the production process and to protect steel vessels against overheating and subsequent mechanical failure [1]. Between all the phenomena to which the refractory lining is exposed during service in the steel industry, the effect of the time-dependent response of the material is crucial in determining the performance of the lining [1,2,3]. The time-dependent behaviour of refractories includes creep and stress relaxation phenomena that are defined by a slow continuous deformation of a material under constant stress and temperature, and a decrease of stress under constant deformation [4], respectively, and which represent the viscous response of the material. When modelling refractory linings, stress accumulation might result in mechanical failure due to the lack of a nonlinear viscous behaviour [2]. Hence the importance of a good representation of the viscous behaviour of refractory materials as to understand and be able to predict structural performance. Since creep and stress relaxation can be modelled through analogous mathematical models [5], it is admissible to refer to creep when referencing viscous behaviour. Furthermore, it is usual to choose one type of experimental protocol to obtain the dataset. Therefore, creep will be the focus of the present work.

Refractories experience significant creep when exposed to high temperatures (in the range of half of the melting temperature) [6], and usually show three characteristic stages. During the first stage, named primary creep, the creep rate declines gradually with time. In the secondary stage, the creep rate is almost constant. Lastly, the third creep stage region is where the creep rate increases and leads to failure [7]. Temperature and stress have a significant impact on creep behaviour: under low temperature and stress conditions, creep might be negligibly small, whereas it develops faster at high temperature and stress conditions [8].

To precisely characterize high-temperature creep behaviour of metals and alloys, considerable efforts have been made to obtain a fundamental understanding of the creep mechanism and to develop creep constitutive models [9], such as the power law equation [10] applied to describe the behaviour of materials up around 1500 °C, the continuum damage equation [11] used to represent metals response about 700 °C, and the theta projection method [12] employed for temperatures up to 1300 °C.

In 1929, Norton [10] proposed the power law equation, further developed with the publication of Bailey’s work [13], forming the Norton-Bailey creep law, which is popular for its simplicity in application to stress analysis. Continuum damage mechanics (CDM) was proposed in 1958 by Kachanov [11]. By selecting appropriate constitutive equations and damage variables, this method was used to estimate the rupture time and strain of components that operate at elevated temperatures. In 1965, the Garofalo equation was introduced to describe the relationship between creep strain rate and time [14]. All the aforementioned models, however, only specify the primary and secondary creep phases. It was only in 1982, with the development of the theta projection method by Evans and Willshire [12] that a description covering all creep processes including the tertiary stage up to rupture was proposed, thus offering a general description of the creep curve. The theta projection method has been successfully employed to describe the creep behaviour of metals and alloys [8, 9, 15,16,17,18], being able to describe the complete creep curve in one equation and allowing more accurate prediction of long-term creep behaviour from the extrapolation of short-term experimental data when compared to other methods [9].

As the creep behaviour of ceramics is similar to metals and alloys [6], the creep response of refractories is commonly represented by models developed for metals. The Norton-Bailey creep model [2, 19,20,21,22] in particular, is one of the most used due to its simplicity, good representation of the creep behaviour for this class of materials, and availability in commercial finite element software codes. However, the Norton-Bailey creep model cannot represent the complete creep curve and it requires the definition of primary and secondary states separately. In addition, creep does not follow one simple power law relationship over a wide range of stress, typically following one power law at low stress levels and another power law at high stress levels—a phenomenon known as “power law breakdown” [23], which does not allow for a generalized application of the Norton-Bailey’s coefficients. Furthermore, the coefficients themselves are highly temperature dependent, thus, complicating the obtention of a representative creep model using a small data set. Finally, the application of the Norton-Bailey creep law for refractories requires different sets of coefficients for each creep stage, stress range, and temperature level, which leads to a lack of generalization that increases the number of model coefficients required, and thus demands an abundant database, hence complicating the numerical simulation of refractory structures.

The theta projection method, on the other hand, can represent the complete creep curve by applying a continuous approach for its coefficients, where equations in terms of stress and temperature define the theta coefficients employed to obtain the creep response over various temperatures and stress levels. Moreover, this creep equation may be implemented in most commercial software through user supplied subroutines. Finally, the theta projection method can accurately predict the material’s long-term creep behaviour from the extrapolation of short-term experimental creep strain data [9]. The cumulative set of factors mentioned justifies the interest in applying the theta projection creep method to represent refractory creep. In the present work, the application of the theta projection creep method is adopted to characterize the compressive creep of alumina-spinel refractories over a range of stresses and constant temperatures levels. The goal is to represent all creep stages and their transition with a single equation while using a few parameters to describe the variation of creep with temperature and stress. Monotonic increase of creep strain with temperature and stress is considered for developing the model. Alumina spinel refractory bricks employed in steel plants, especially in the working lining of steel ladles, were studied in this work. This work was developed within the scope of ATHOR Project [24], a Marie Skłodowska-Curie Action European Training network dedicated to Advanced THermomechanical multiscale mOdelling of Refractory linings, and therefore the material studied was defined according to the guidelines of the project. The alumina-spinel material is described in Sect. 2 together with the creep data set utilized. Considering the small quantity of creep data available for this material, two data sets originating from different test protocols were combined. Section 3 presents a review of the theta projection method and its evolution, followed by the definition of the model applied in this work and the description of the fitting process. In Sect. 4, the performance of the model is presented and the implications of its use are discussed. Final remarks are presented in Sect. 5.

2 Material and experimental creep tests

2.1 Investigated material

According to the alumina spinel brick’s technical data sheet [25], the bricks' raw materials include white fused alumina, calcined alumina, and spinel. The bricks used here were composed of 94% Al2O3, 5% MgO, 0.3% SiO2, and 0.1% Fe2O3 [25]. The bulk weight was 31.3 kN/m3, and the open porosity was 19 vol% [25]. In the scope of ATHOR Project [24] the alumina spinel bricks were amply characterized [26,27,28,29,30,31]. The material’s dynamic Young’s modulus evolution with temperature [28] obtained through ultrasonic pulse velocity tests is presented in Fig. 1 and will be employed in the evaluation of the creep law. This choice was made since ultrasonic measurements can define instantaneous Young’s modulus, while in static mechanical tests, the static load is applied slowly, thus receiving interference from time effects such as creep at high temperatures. The Poisson’s ratio is 0.3 and the thermal expansion coefficient is \(8.9 \cdot {10}^{-6}{^ \circ {\rm C}}^{-1}\) [31].

Fig. 1
figure 1

Alumina-spinel Young's modulus evolution with temperature (adapted from [28])

Full size image

2.2 Uniaxial compressive creep strain tests

Two types of testing procedures were employed to characterize the creep behaviour of the alumina spinel refractory bricks studied in this work: steady-state temperature creep tests and transient temperature creep tests. In the steady-state temperature creep tests, Fig. 2a, the specimen was heated until it reached thermal equilibrium under a predefined maximum temperature. At this stage, the mechanical load was applied, and the deformation started to be measured. In the transient creep tests, shown in Fig. 2b, the specimen was loaded before heating to a predefined maximum temperature, and the deformation was measured from the moment when the mechanical load started to be applied.

Fig. 2
figure 2

Experimental protocol: a steady-state tests, b transient temperature tests

Full size image

The test protocol and the creep data used in this work will be presented in subsequent sections. Both data sets were gathered within ATHOR network [24]: the steady-state creep data was developed by ATHOR colleagues in Montanuniversitaet in Leoben and reported in detail in Samadi et al. [32], while the transient data is novel and will be presented next.

2.2.1 Steady-state temperature creep tests

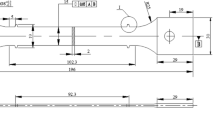
Samadi et al. [32] presented a steady-state temperature creep data set for alumina-spinel refractories, obtained by following a methodology developed by Jin et al. [19] for uniaxial compressive creep tests. The testing machine of [19] measures the displacements developed during the creep testing using two extensometers positioned on the front and rear sides of the furnace, with an initial distance between them of 50 mm. The entire sample is located inside the furnace, together with the upper and the lower pistons. A schematic representation of the compressive creep experimental setup is presented in Fig. 3.

Fig. 3
figure 3

Setup of the steady-state temperature compressive creep test (adapted from [19])

Full size image

The samples used in this test are solid cylinders with 35 mm in diameter and 70 mm in height. At the beginning of the test, after their placement in the testing apparatus, a compressive preload of 0.05 MPa was applied to hold the specimen in place during the heating process. A cylindrical electrical furnace was employed to heat the specimen to the desired temperature at a rate of 10 °C/min. To ensure thermal homogenization, a dwell period of 1 h was applied. Afterwards, the defined testing force was applied to the specimen, and only at this moment, the displacement started to be measured. This implies that the deformation results did not include temperature effects, comprising only elastic and creep strain. The loading cases studied are presented in Table 1. For each case of applied stress at a given temperature, three specimens are tested.

Table 1 Loading conditions for steady-state temperature creep tests
Full size table

The complete compressive creep curves obtained experimentally at the three different temperatures and stress levels are presented in Fig. 4. It is possible to observe that for each temperature level, creep strain increases with the increase of applied stress, as expected. Considerable scatter in the data can be observed. Figure 4a, for example, shows that, for the material studied in this work, under a compressive stress of 8 MPa at 1300 °C, one specimen failed after 11.5 h, while another one failed after 3 h, a considerable difference. The dispersion in the data is normal for refractory materials and can be explained by many factors [3]. From a material standpoint, the production processes, such as pressing and heat treatment, may be responsible for heterogeneity in the bricks used to create the samples. With an aggravation that refractories often have large grain sizes, around 10 mm [32], in comparison to the size of mechanical test samples. Regarding the testing methodology, variations in the results might be caused by the presence of micro-cracks in the sample. Those can occur during the sample’s production or be caused by misalignment of the load [3]. Although there exists a considerable scatter in the data sets, it is possible to observe a consistent tendency in the mean creep curves concerning the temperature and stress levels.

Fig. 4
figure 4

Steady-state temperature creep tests results: a 1300 °C, b 1400 °C, and c 1500 °C

Full size image

2.2.2 Transient temperature creep tests

The experimental campaign for the determination of creep in compression under transient temperature was carried out at RWTH Aachen University, following the methodology proposed in ISO 3187 [33]. The setup scheme of the test is presented in Fig. 5. The measurement of temperatures is made at two different points through thermocouples that are installed near the specimen to monitor its temperature, and near the heating elements to control the furnace temperature. The specimens employed were cylinders with a diameter of 50 mm and a height of 50 mm. Because of the differential measuring system adopted for the determination of deformation, the cylindrical test pieces have co-axial holes of 12.5 mm diameter. The differential displacement of two corundum tubes through linear variable differential transducers (LVDTs) is used to measure the change in length of the specimen. After the specimen is placed in the testing apparatus, a compressive load is applied when the furnace is turned on, causing a permanent compressive stress of 0.2 MPa throughout the entire experiment. The specimen is heated by the electrical furnace up to the desired temperature (1150, 1200, 1380, 1450 or 1500 °C according to Table 2) with a rate of 2 °C/min followed by a dwell period of 50 h. The deformation measurement started simultaneously with the initial mechanical loading procedure. Therefore, the displacement measured includes elastic deformation, thermal expansion, and creep strain. For each temperature, only one specimen was tested.

Fig. 5
figure 5

Setup of the transient temperature compressive creep (adapted from [29])

Full size image
Table 2 Loading conditions for transient temperature creep tests
Full size table

The results obtained in terms of strain evolution in time are presented in Fig. 6. For each temperature test, the experimental strain and the temperatures were measured at the centre of the specimens. In addition, a curve with the sum of elastic strain \(\sigma /E\) generated by the mechanical stress of 0.2 MPa and thermal \(\left(\alpha \Delta T\right)\) expansion is shown to aid in the description of results.

Fig. 6
figure 6

Transient temperature creep test results: a 1150 °C, b 1200 °C, c 1380 °C, d 1450 °C and e 1500 °C

Full size image

Figure 6a refers to the test with a dwell temperature of 1150 °C. Observing the total experimental strain and the thermoelastic strain curve, it becomes clear that the creep developed during the heating procedure is rather negligible, as both curves overlap. It is only with the start of thermal dwell, marked by the vertical line (A) that non-negligible creep is generated. The creep developed while the temperature was held constant is represented by \({\Delta \varepsilon }_{crCT}\). For this temperature a modest value of approximately \(3\cdot {10}^{-4}\) was developed over 50 h, as shown in point (B). This remark corroborates the hypothesis that alumina-spinel refractories begin to develop non-negligible viscoelastic behaviour at around 1100 °C [34]. The results for the specimen with a maximum temperature of 1200 °C, shown in Fig. 6b, reinforce this hypothesis as the occurrence of creep strain becomes noticeable only after thermal equilibrium is attained (vertical line (A)). But differently from the results of 1150 °C the creep curve is well developed in its shape, producing a creep strain of \(1.5\cdot {10}^{-3}\) (point (B)). From the observation of the results for 1380 °C shown in Fig. 6c, the start of the development of non-negligible creep strain is marked by the deviation of the total strain experimental curve from the thermoelastic one at 1150 °C, represented by the vertical line (A). The difference between the thermoelastic curve and the actual observed behaviour up to the end of the heating-up procedure, represented by the vertical line (B), is caused by compressive creep effects, which will be referenced as transient-temperature creep and represented by \({\Delta \varepsilon }_{crTT}\). A transient-temperature creep strain of approximately \(1.1\cdot {10}^{-3}\) (point (C)) is developed in the 1.3 h it takes for the temperature to go from 1150 to 1380 °C. In the following 50 h dwell period, the creep strain developed is approximately \(4.6\cdot {10}^{-3}\) (point (D)). The total creep developed during the experiment is represented by the sum of transient-temperature creep (\({\Delta \varepsilon }_{crTT}\)) and the creep developed under constant temperature (\({\Delta \varepsilon }_{crCT})\). The same trend is repeated for 1450 and 1500 °C. The results for 1450 °C presented in Fig. 6d, show that during the 2.9 h needed for the temperature to increase from 1150 to 1450 °C, a creep strain of \(2.7\cdot {10}^{-3}\) is developed (point (C)). Followed by the development of \(5\cdot {10}^{-3}\) (point (D)) during the 50 h dwell period. Figure 6e shows the results for 1500 °C, where the transient creep strain is \(3\cdot {10}^{-3}\) (point (C)) and the creep developed under constant temperature is \(5.7\cdot {10}^{-3}\) (point (C)). In the test results with a maximum temperature of 1450 and 1500 °C it is possible to note that around 1300 °C, represented by point (E), the total experimental strain reaches a maximum value and starts to decrease, which means that at this point the increment of compressive creep strain generated is higher than the increment of thermal strain, thus decreasing the total strain measured.

Considering for calibration only the creep strain developed under constant temperature would imply an underestimation of the creep strain since the creep developed under transient temperature would not be represented. The strategy proposed in this work to minimize the effects of this implication in the curve used in the calibration process is to consider the creep developed during the heating procedure. Figure 7 illustrates the change of the coordinate system performed to obtain the data referent to the compressive creep strain under constant temperature. Initially, the origin of the axis is shifted to the point from which thermal equilibrium is attained within the specimen (\(\mathrm{I}\to \mathrm{II}\)). In the sequence, the term \({\Delta \varepsilon }_{crTT}(T)\) representing the totality of creep developed under transient temperature conditions and shown in Fig. 6 for each dwell temperature test is added to all points (\(\mathrm{II}\to \mathrm{III}\)). The compressive creep results that will be employed for the calibration purpose in this work are presented in Fig. 8. All the results from transient temperature creep tests presented in the following sections will be presented in the treated form.

Fig. 7
figure 7

Process of data treatment of the transient temperature creep tests results

Full size image
Fig. 8
figure 8

Transient temperature creep tests results under constant temperature

Full size image

3 The theta projection method

3.1 Classical and modified theta projection methods

The theta projection model was originally proposed by Evans and Willshire [12] to simulate multistage creep deformation (primary, secondary, and tertiary), and accurately predict long-term creep behaviour. The theta creep strain formulation under constant temperature and stress is presented in Eq. (1).

$$\varepsilon _{{cr}} = \theta _{1} \left( {1 - e^{{ - \theta _{2} t}} } \right) + \theta _{3} \left( {e^{{\theta _{4} t}} - 1} \right)$$
(1)

Here, \({\varepsilon}_{cr}\) is the creep strain, \(t\) is time and \(\theta_{i}(i=1,2,3,4)\) are non-negative model parameters, named theta coefficients. Primary creep strain is controlled by the material constants \(\theta_{1}\) and \(\theta_{2}\), while material constants \(\theta_{3}\) and \(\theta_{4}\) regulate the tertiary creep.

The format of the curve defined by Eq. (1) and the influence of each term on the shape of the curve are illustrated in Fig. 9. The first term on the right-hand side of Eq. (1) is appropriate to represent the primary creep strain, as it increases slowly over time while the slope progressively decreases to zero. The parameter \(\theta_{1}\) represents the total primary creep strain while \(\theta_{2}\) determines the shape of this component. The second term of the equation is suitable to represent the tertiary stage, as it starts negligibly small and then grows exponentially with time. In it, the parameter \(\theta_{3}\) scales the tertiary creep strain while \(\theta_{4}\) defines the curvature [15]. An approximate stable creep strain that might correspond to secondary creep is obtained during the change in dominancy from the first term to the second term [8]. Furthermore, the material constants \(\theta_{i}\) (\(i=1,2,3,4\)) are both temperature (\(T\)) and stress (\(\sigma\)) dependent. The relation between \(T,\sigma\) and \(\theta_i\) was originally proposed by Eq. (2) [35].

$$\ln \left( {\theta_{i} } \right) = a_{i} + b_{i} \sigma + c_{i} T + d_{i} \sigma T$$
(2)
Fig. 9
figure 9

Illustration of theta-projection method (adapted from [36])

Full size image

Here \({a}_{i}\), \({b}_{i}\), \({c}_{i}\) and \({d}_{i}\) (\(i=\mathrm{1,2},\mathrm{3,4}\)) are material constants.

To better accommodate the experimental data for different materials, variations of the original theta projection model have been developed. Those models are called a “modified theta projection model” and might differ from the original model in various ways. Some of the modified models include an extra linear [36] or exponential [18, 37] term to the theta projection creep equation. Another modification, contrary to the original theta projection model, expressed the creep strain as a logarithmic function [17]. In addition, different correlations were proposed to define the material constants \({\theta }_{i}\). A few proposals adopt mechanical parameters in the definition of material constants [16, 38, 39]. In a study by Evans [40], various interpolation/extrapolation functions for the theta coefficients within the theta projection technique are evaluated, and a more generalized function for the material constants \({\theta }_{i}\) is proposed. The new correlation proposed is presented in Eq. (3).

$$\ln \left( {\theta_{i} } \right) = a_{i} + b_{i} \frac{1}{T} + c_{i} \frac{\sigma }{T} + d_{i} \ln \left( \frac{1}{T} \right) + e_{i} \sigma$$
(3)

Again, here, \({a}_{i}\), \({b}_{i}\), \({c}_{i}\), \({d}_{i}\), and \({e}_{i}\) (\(i=1,2,3,4\)) are constants.

3.2 Theta projection model applied to refractories

In this work, the original function proposed by Evans and Willshire [12] in Eq. (1) was applied to model the creep behaviour of the alumina-spinel refractories at high temperatures. The choice was made considering the good agreement between the experimental data studied here and the proposed equation. On the other hand, the material constants \({\theta }_{i}\) (\(i=1,2,3,4\)), which are both temperature (\(T\)) and stress (\(\sigma\)) dependent, were chosen to be fitted according to the general form of Eq. (3) proposed by Evans [40].

3.3 The fitting process/Identification of creep parameters

The procedure of the overall methodology development of this study is presented in Fig. 10. In the experimental part, a total number of 32 specimens were used for the uniaxial compression creep testing at temperatures ranging from 1150 to 1500 °C with holding stresses of 0.2–10 MPa. The total strain vs. time data was acquired for each of the specimens. There is one data set of 27 steady-state temperature creep tests composed of experiments in three temperature levels. For each temperature, three distinct mechanical loads were investigated. Finally, each temperature and load combination was repeated three times. The other data set was formed by data from a single mechanical load tested over five temperature levels obtained from transient temperature creep tests. The use of one data set to calibrate the creep model and the other to validate would be usually adequate. Here, however, it would implicate the construction of a model using a restricted data set in terms of size, and range of stress and temperatures, which could lead to restrictions in the applicability of the model.

Fig. 10
figure 10

Overall diagram of creep testing, model development, validation, and comparison

Full size image

Hence, data originating from both data sets will be used to calibrate the theta projection creep model. For that, some simplifications needed to be adopted. The samples used in the tests, for example, are different, but considering that both their sizes are representative of the alumina-spinel matrix, the differences caused by size and shape may be disregarded. Another point to be addressed regards the repeatability of the tests, or lack of evidence of it, in the case of the transient temperature creep tests. As observed in the steady-state results, there is a considerable difference in the behaviour of repetitions of equal specification in equal conditions. Therefore, there exists a range of acceptable results for comparison purposes. This does not exist for the cases in which only one test was executed during the calibration process.

The calibration of the creep model is implemented in two stages: in the first stage a set of theta coefficients \({\theta }_{i}(T,\sigma )\) are obtained for each case of applied stress at a given temperature. In the second stage, a continuous function is fitted to generalize the definition of \({\theta }_{i}\) over a range of temperatures and stress. Finally, the obtained results are validated against the experimental data.

As two different types of data sets were merged: one from the steady-state temperature creep tests and the other from the transient temperature creep tests, different pre-treatments were employed to obtain the creep strain data. As mentioned before, the measured results for the steady-state temperature tests comprise both elastic and creep deformation. Therefore, to obtain the creep strain \({\varepsilon }_{cr}\), the elastic strain \(\sigma /E\) is subtracted from the total strain \({\varepsilon }_{tot}\) obtained experimentally, as:

$$\varepsilon_{cr} = \varepsilon_{tot} - \frac{\sigma }{E}$$
(4)

where σ is the applied stress and E is Young’s modulus obtained from Fig. 1.

The original transient creep test results contained thermal, elastic, and creep deformation. The treatment to obtain the compressive creep data was presented in Sect. 2 and illustrated in Fig. 7. It included the subtraction of both elastic \(\sigma /E\) and thermal strain \(\left(\alpha \Delta T\right)\) using Eq. (5). Furthermore, the origin of the axes was shifted to the instant in which thermal equilibrium was attained, and the term \({\Delta \varepsilon }_{crTT}(T)\) was added to all the entries of the shifted data.

$$\varepsilon_{cr} = \varepsilon_{tot} - \frac{\sigma }{E} - \alpha \Delta T$$
(5)

Finally, the database is compiled with time versus creep strain data at constant temperatures. From the transient temperature creep tests, the experiments with maximum temperatures of 1200, 1380, 1450, and 1500 °C were employed in the calibration procedure. The results for the experiment with a maximum temperature of 1150 °C were disregarded since creep starts developing around this temperature and the creep values are almost negligible.

3.3.1 Creep strain model

The material constants \({\theta }_{i}\) are obtained from uniaxial testing data at constant stress and temperature. The nonlinear least square method [41] is applied to obtain suitable \({\theta }_{i}\) values. In this method, the \({\theta }_{i}\) coefficients are obtained by minimizing the error between the experimentally obtained creep curves and those predicted using Eq. (1) represented by Eq. (6). The native MATLAB [42] function lsqcurvefit is used to minimize the function presented in this equation. During the fitting, a constraint was applied that all \({\theta }_{i}\) values should be positive. In addition, for the creep tests at the same temperature, tests with higher stress loads were restrained to give higher fitted model parameter \({\theta }_{i}\). The first constraint generally guarantees that three terms represent the primary, secondary and tertiary stages properly, while the latter one assures that under the same temperature, creep strain monotonically increases with stress load. Furthermore, to avoid the effect of weights caused by different-sized data sets in the data-fitting procedure, subsets of data were created with the same number of points from the smallest data set available for each case. The sizes of the subsets vary between 3000 to 25,000 points, with more points on the tests that lasted longer.

$$\varphi^{n - 1} = \mathop \sum \limits_{i = 1}^{n - 1} \left\{ {\varepsilon_{cr i} - \left[ {\theta_{1} \left( {1 - e^{{ - \theta_{2} t}} } \right) + \theta_{3} \left( {e^{{\theta_{4} t}} - 1} \right)} \right]} \right\}^{2}$$
(6)

Here, the creep curve contains \(n\) time points and \({\varepsilon }_{cr i}\) is the experimental creep strain at the time \({t}_{i}\). An iterative algorithm based on the trust-region-reflective method [43] was used to find optimum values for \({\theta }_{i}\) which minimize \({\varphi }^{n-1}\).

3.3.2 Temperature and stress dependence model

The theta coefficients \({\theta }_{i}\) obtained for each experimental curve are dependent on the applied stress and temperature. Therefore, they must then be related to the applied test condition using a suitable function, which results from Eq. (3).

$$ln\left( {\theta_{i} } \right)_{k} = a_{i} + b_{i} \frac{1}{{T_{k} }} + c_{i} \frac{{\sigma_{k} }}{{T_{k} }} + d_{i} \ln \left( {\frac{1}{{T_{k} }}} \right) + e_{i} \sigma_{k} , i = 1,4$$
(7)

Here, \({a}_{i}\), \({b}_{i}\), \({c}_{i}\), \({d}_{i}\), and \({e}_{i}\) (\(i=1,2,3,4\)) are material constants obtained from \(k\) creep experiments, with applied stress and temperature of \({\sigma }_{k}\) and \({T}_{k}\), respectively. Suitable \({a}_{i}\), \({b}_{i}\), \({c}_{i}\), \({d}_{i}\), and \({e}_{i}\) values are obtained by minimizing the error between the obtained theta coefficients \({\theta }_{i}\) and those predicted using Eq. (7). The native MATLAB [42] function lsqcurvefit is once again used to perform this minimization process.

In Fig. 11, the overall two-stage procedure to calibrate the theta projection creep model is summarized. It is important to note that the second stage of the calibration procedure is independent of the first stage and is carried out in order to obtain generalized values for the \({\theta }_{i}\) coefficients.

Fig. 11
figure 11

Evaluation procedure to calibrate the theta projection creep model

Full size image

4 Results and discussion

Using the approach described, the proposed model and the identification of creep parameters procedure were implemented in MATLAB. Predicted creep curves were compared with experimental data. The efficiency of the model is discussed in two instances: regarding the first stage of calibration, where the material constants \({\theta }_{i}\) were directly obtained, and the effectiveness of the temperature and stress-dependent model to reproduce the experimental data. Finally, the material constants \({\theta }_{i}\) derived functions are debated and the influence of the data set is discussed.

The material constants \({\theta }_{i}\) (i = 1, 2, 3, 4) under different temperatures and stresses that satisfy Eq. (1) are presented in Table 3. Figure 12 illustrates the predicted theta projection creep curves compared with the experimental data. The experimental results are presented in colours, while the numerical estimation is presented in black. For the cases where three specimens were tested, the experimental results are presented through a shaded area. Generally, the three stages of the creep process were demonstrated by the curves with the creep strain rate decreasing at the early stage, then stabilizing, and finally increasing. Tertiary creep is insufficiently replicated when compared to experimental results, therefore it should be further investigated for applications in which collapse is more representative than the case of the refractory used in the lining of steel ladles. Still, good agreement was achieved between the model predictions and experimental data for all the curves, in the rest of the response.

Table 3 Model parameters for alumina-spinel refractory
Full size table
Fig. 12
figure 12

Creep simulation predictions compared with experimental creep tests at a 1200 °C, b 1300 °C, c 1380 °C, d 1400 °C, e 1450 °C and f 1500 °C

Full size image

The final step of the calibration process is the definition of the temperature and stress dependence model for the theta parameters previously obtained. Based on Eq. (3), the \({a}_{i}\), \({b}_{i}\), \({c}_{i}\), \({d}_{i}\), and \({e}_{i}\) (\(i=1,2,3,4\)) coefficients for each \({\theta }_{i}\) were calculated, and their values are given in Table 4. The importance of this model resides in its generalization capability. Based on the obtained database, it becomes possible to propose a creep model that should work for a wide range of stress and temperature load conditions (except tertiary creep), which is valuable in the numerical simulation of the material behaviour of refractories.

Table 4 The \({a }_{i}\), \({b }_{i}\), \({c }_{i}\), \({d }_{i}\), \({e }_{i}\) (i = 1,2,3,4) coefficients for each \({\theta }_{i}\) based on Eq. (3)
Full size table

The surface functions of \({\theta }_{i}\) (i = 1,2,3,4) are presented in Fig. 13, together with the original values of the theta parameters obtained in the first stage of the calibration process, and the distance between them and the fitted surface (given by the arrows shown). In general, the temperature and stress dependence of the coefficients is strong. Additionally, an increment in stress will produce different variations in \({\theta }_{i}\) coefficients according to the temperature level. Higher temperatures imply greater variations, which confirms that creep phenomena are exacerbated with temperature increases and agrees with the hypothesis of a monotonic increase of creep strain with temperature and stress. Finally, it is important to comment on the implication of the characteristics of the data set on which the surface is based. The nonlinear regression is used to fit the data into an equation that can be used to make predictions. In the optimal scenario, there will be enough points in the data set for it to be split into two groups: one to fit the equation and the other to validate the result. For nonlinear functions, for example, it is usual to employ a minimum of three points over different orders of magnitude to fit an equation. Considering that the creep data set used in this work has a maximum of four mechanical loads tested for each temperature level, it is complicated to split the dataset into two to define the nonlinear function and assess its performance. Moreover, the load levels applied for each temperature stage have small deviations, which might compromise the fit of the function and hamper the efficiency of the function across a wide range of stresses. Furthermore, when comparing the stresses applied at different temperatures in the dataset, they vary significantly (e.g. 1300 °C compared to the other levels), or they do not change much (1400 to 1500 °C), hence making it difficult to assess the implications to the predictive capabilities of the model.

Fig. 13
figure 13

Temperature and stress dependence model fit for \({\theta }_{i}\) coefficients, across the relevant stress and temperature ranges

Full size image

The error between the original values of the \({\theta }_{i}\) coefficients and the estimated \({\theta }_{i}\) parameters are inherent to the fitting process and may be caused by the scattering of the creep data. The relative error between the \({\theta }_{i}\) coefficients are below 10 for 85% of the points compared. The 15% remaining points have relative errors ranging between 22 and 137% and refer to \({\theta }_{3}\), which suggests an incompatibility between the data and the proposed temperature and stress dependence function for the coefficient \({\theta }_{3}\), or the presence of outliers. Still, the results may also indicate some lack of aptitude of the model in representing the third-stage creep and failure for the alumina-spinel refractory.

The final estimation of creep strain using a global model across a relevant range of temperatures and stress levels is made through Eq. (1) using the constants in Table 4, which are applied in Eq. (3), to obtain the \({\theta }_{i}\) coefficients. The final theta projection prediction results are shown in Fig. 14. The obtained curves agree well with the experiments, although the global fitting of the \({\theta }_{i}\) coefficients alter the values and shape of the curves at the experimental reference values. At 1300, 1400, and 1500 °C the theta projection curves are mostly within the range of experimental results, and the existing deviations are not significant when compared to the scatter of the test results. For the transient temperature creep tests, the results can still be considered in reasonable agreement even if some difference is found. As there is no repetition of the experimental results, it is impossible to conclude if the result is a lower or upper bound. Finally, it is possible to infer that the temperature and stress dependent model combined with the original theta projection creep equation represents well the experimental creep behaviour trend of alumina-spinel refractories.

Fig. 14
figure 14

Final theta projection creep predictions compared with experimental creep tests at a 1200 °C, b 1300 °C, c 1380 °C, d 1400 °C, e 1450 °C and f 1500 °C

Full size image

At last, the final theta projection creep predictions are compared to the Norton-Bailey creep estimates for 1300 °C. Using the Norton-Bailey creep parameters presented by Samadi et al. [32], and the exact integration of the Norton-Bailey creep equation, the comparison of creep tests at 1300 °C is presented in Fig. 15. The experimental results are presented in colours, the theta projection creep predictions are presented in black, and the Norton-Bailey results are presented in red. In detail, it is possible to observe that the Norton-Bailey creep predictions present good results for primary stage creep, which is expected since the parameters are calibrated regarding primary stage data. On the other hand, the overall shape of the Norton-Bailey creep curve is unable to grasp the evolution of a complete creep curve which confirms that this model is capable only of representing individual stages. Differently, the theta projection creep curves present a much better fit to the complete curve. For the other temperatures, the same trend is expected.

Fig. 15
figure 15

Final theta projection creep predictions compared with Norton-Bailey creep predictions at 1300 °C

Full size image

5 Conclusions

Creep is an important phenomenon to be considered in materials forming structures exposed to high temperatures and stresses. At service conditions in industrial vessels, the creep deformation experienced by refractories is one of the most important phenomena when addressing the life cycle of the material, as well as the definition of the initial geometry of the refractory bricks and the heating time of the vessel. Hence, a good creep model for alumina-spinel refractories is needed for efficiency and safety analysis of the vessels.

In the present study, the theta projection method is adapted for alumina-spinel refractories. The theta projection creep model represents the complete creep curve, particularly primary and secondary creep, which are the relevant phenomena for refractory applications. In the model, creep curves are described as a function of time with four model parameters \({\theta }_{i}\) (\(i=1,2,3,4\)). An initial data set of model parameters was constructed by fitting the results of 32 creep tests, run at 6 temperatures, from two different test protocols. After fitting the individual curves, the theta values \({(\theta }_{i})\) were fit to create a unified creep model enabling the determination of creep curves for distinct temperature and stress loads. The fitting process employing the nonlinear least square method was automated using MATLAB [42] to find the minimum of a nonlinear multivariable function. The use of steady-state in combination with transient temperature creep data to calibrate the theta projection creep model enabled the generated model to correctly replicate the results from both types of tests. The predictions of the unified model were in good agreement with the experimental results in most load cases. Compared to other creep models applied to represent the alumina-spinel creep behaviour, this model has the large advantage of a general prediction of creep over a wide range of stresses and temperatures, with good agreement with experimental data. Moreover, the unified approach adopted led to the development of a more consistent and universal creep model, which is prepared for further development, such as the inclusion of improvements to better represent creep under transient temperature and the effects of the tertiary creep stage. Finally, further experimental data and numerical studies on the numerical application of this model are necessary before employing this model in the numerical analysis of refractory structures to define operating conditions and safety levels.