Siteswap

Aquellos que hayan visitado un campus universitario no habrán tenido mucha dificultad para encontrar estudiantes pasando el rato jugando a los malabares. Otra cosa fácil de encontrar en una universidad es empollones de todo tipo. En algunas ocasiones incluso ambos personajes resultan ser el mismo: un empollón malabarista. Y un empollón malabarista es precisamente lo que era Paul Klimek, que además de tener gran habilidad con las bolas era matemático en la Universidad de California en Santa Cruz.

Klimek, y posteriormente otros matemáticos, desarrollaron una notación numérica para trucos de malabares conocida como notación Siteswap (también llamada a veces Quantum Juggling o Cambridge Notation), que además de simple es bastante bonita.

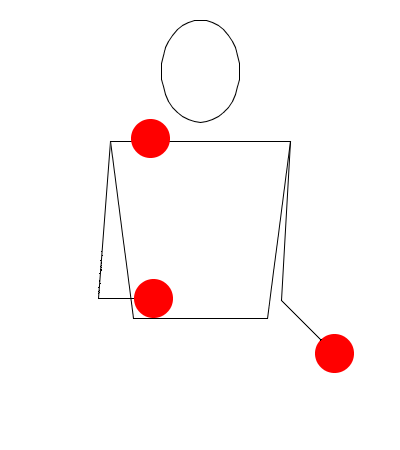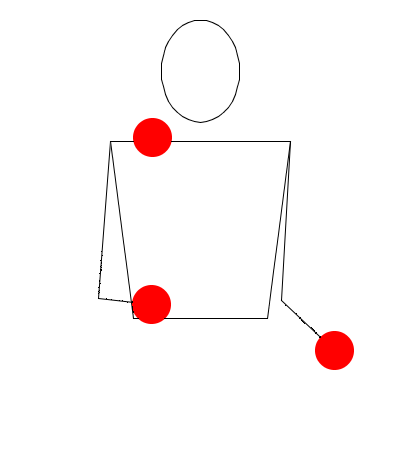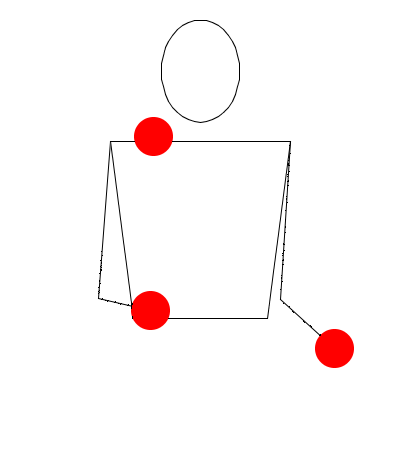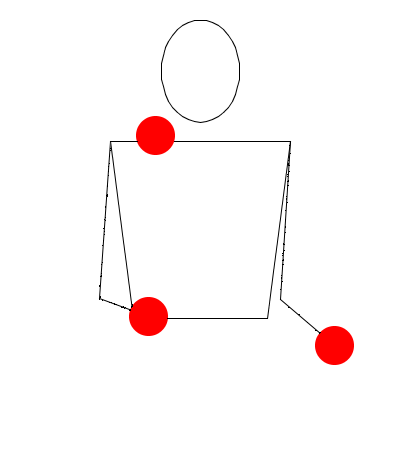
La idea consiste en registrar la acción de cada mano en una secuencia temporal, como si las manos actuasen por turnos (izquierda, derecha, izquierda, derecha, …). Se visualiza mejor mediante un diagrama como este, en el que se supone que el tiempo “fluye” de arriba a abajo:

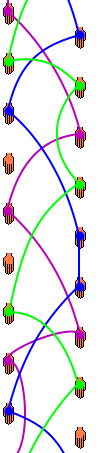
Las acciones posibles son mano vacía, mano con bola, o lanzar bola (a diferentes alturas y cambiando o no de mano).

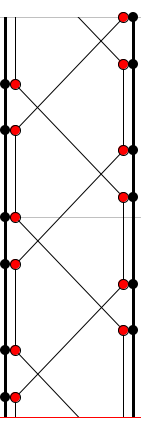
Cada acción se puede codificar con un número entero, contando para ello el número de pasos durante los cuales la bola se mantendrá en el aire. Lo mejor es verlo en un ejemplo:

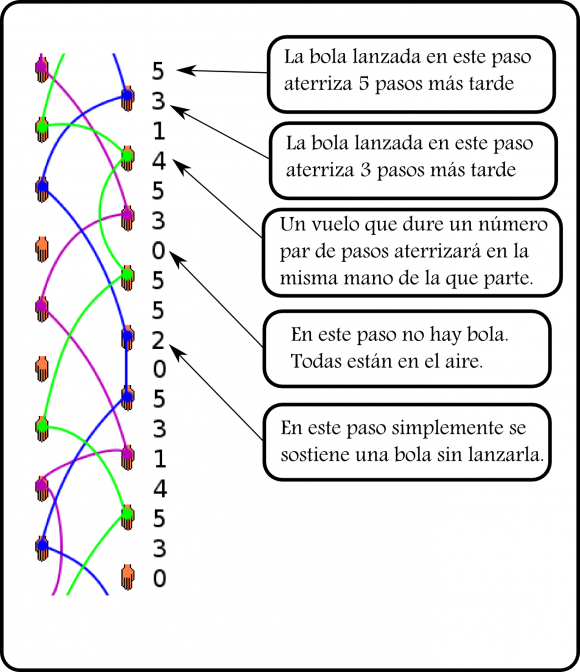
El siguiente diagrama también puede ser útil:

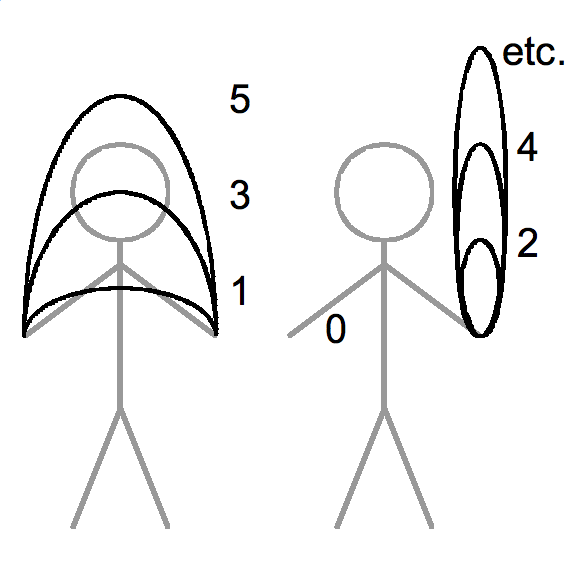
Vemos algunas características de esta notación:

• Cuando aparece un número par, la bola se recogerá con la misma mano con la que es lanzada.
• Si es impar, la bola cambiará de mano.
• El número tiene que ver con el tiempo que pasa volando la bola, y por tanto con la altura a la que se lanza
• Un 0 representa una mano sin bola, y un 2 una mano que sostiene una bola sin lanzarla.

Hay que aclarar que normalmente los trucos no son tan complicados como el de este ejemplo. Habitualmente son secuencias muy cortas, como por ejemplo 333 o 40, y se da por hecho que se repiten periódicamente.

Llegados a este punto, y suponiendo que el lector no haya desistido antes, se podría pensar que la notación Siteswap es solamente un artificio descriptivo, un enrevesado y tedioso tour de force. Una acusación muy habitual en matemáticas.

Los más entusiastas estarán esbozando una sonrisilla, pues habrán han vislumbrado conceptos de matemática discreta y teoría de grafos asomándose tras todo lo expuesto.

No lo demostraremos aquí, pero utilizando teoría de grafos podemos sacarle mucho partido a la notación Siteswap. Por ejemplo, un simple vistazo a la secuencia Siteswap de un truco nos permite:

• Saber cuántas bolas son necesarias para hacer el truco: su número coincide con la media aritmética de la secuencia.
• Saber si el truco es factible: por ejemplo, el truco 41 no es factible, pues su media aritmética es un número fraccionario, y no podemos jugar con un número fraccionario de bolas.
• Diseñar nuevos trucos: al ser muy fácil saber de antemano si un truco será factible o no, el proceso de “lo voy a intentar a ver si me sale” se acelera bastante. Un modo fácil de diseñar nuevos trucos es tomar una secuencia Siteswap válida y permutar sus elementos.

La notación es lo suficientemente sólida como para poder ser utilizada como “lenguaje de programación” de trucos. Existe una multitud de programas dedicados a generar animaciones con un truco concreto a partir de su secuencia Siteswap, de modo que el potencial malabarista pueda saber de antemano no solamente si el truco es factible o no, sino también qué efecto visual tendrá dicho truco.

Más recientemente se han propuesto mejoras a esta notación que añaden al asunto toda la complejidad que uno pueda imaginarse, desde lanzamientos con rebote, malabares a 4 o 6 manos, lanzamientos por detrás de la espalda, etcétera. A título de ejemplo de cómo puede complicarse el asunto, veamos un diagrama para tres malabaristas:

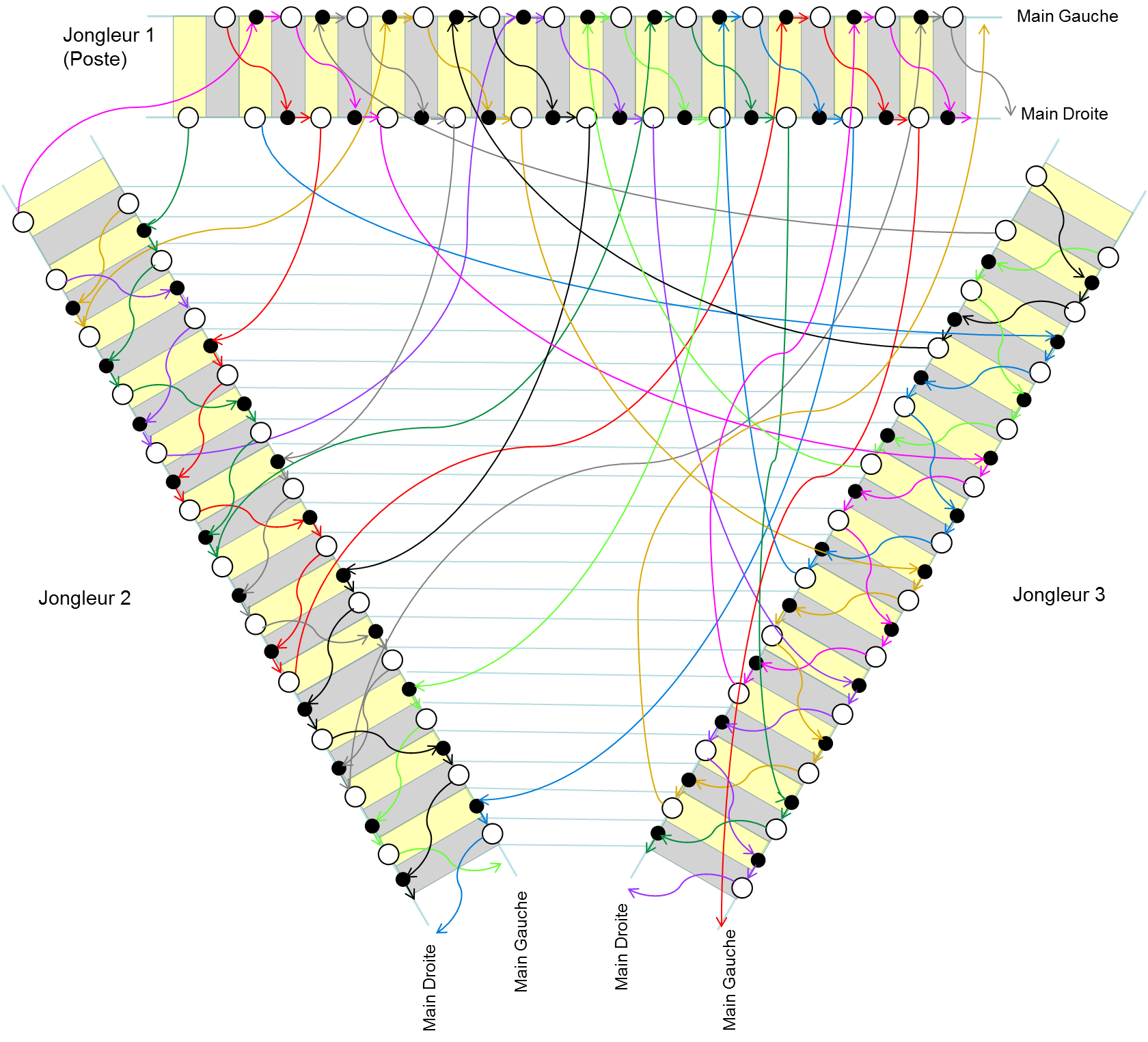
Pero con esto ya hemos tenido bastante por hoy. Me doy por satisfecho si he logrado despertar la curiosidad del lector, que podrá encontrar mucha más información en los links aportados al final del artículo.

Y como propina por haber aguantado hasta aquí, les dejo un cotilleo:

Una nota personal

Hay una anécdota sobre mi relación personal con las matemáticas y los malabares que creo que puede resultar interesante al lector, especialmente si es estudiante. Puedo decir que de no ser por los malabares, seguramente me hubiera alejado hace años del mundo de la ciencia.

Me explicaré, pasen y vean:

Las matemáticas fueron para mí un durísimo trance en mis tiempos del instituto. Estuve suspendiéndolas (y con razón) durante toda la ESO y buena parte del bachillerato, y necesité la paciente ayuda de profesores particulares durante 3 años.

A pesar de mi torpeza en la materia, por algún extraño motivo era consciente de que las matemáticas eran una herramienta fundamental para comprender el mundo. Me resultaban dificilísimas, pero a la vez sumamente atractivas. Además, ya entonces me sentía muy inclinado hacia la física (asignatura que, inexplicablemente, se me daba de maravilla).

Simultáneamente, en aquellos años me introduje, como hobby, en el mundillo del circo. Trabé amistad con una asociación de saltimbanquis de mi ciudad, y aprendí a hacer montones de trucos de malabares, equilibrismo e ilusionismo.

Se trata solo de una apreciación personal, pero lo cierto es que establecí un paralelismo muy claro entre el deseo de aprender matemáticas y el deseo de aprender un nuevo truco. Ambas cosas parecen imposibles hasta que se hacen… y lo cierto es que puede hacerlas cualquiera, y con menos esfuerzo del que imagina.

Terminó el instituto y llegó la hora de elegir una carrera universitaria. El miedo al fracaso, y los consejos de algunos de mis mayores, me hacían dudar sobre si debería o no escoger una carrera con tanta carga matemática como es la licenciatura en física.

En aquellos días del año 2002, por otra parte, estaba practicando un truco nuevo bastante espectacular (un 333, usando machetes de dos palmos). Era difícil, visto desde fuera parecía imposible, además de peligroso y poco aconsejable… me recordaba a la idea de estudiar física. Cuando por fin lo conseguí, decidí que no había nada lo suficientemente difícil, ni para mí ni para nadie, idea que mantengo firmemente 12 años después.

Me atreví. Con tres cuchillos sobre volando sobre mi cabeza, decidí que estudiaría física.

Fue el “más difícil todavía” más relevante de mi vida.

Para la elaboración del presente artículo me he ayudado de Juggling Lab, de Jack Boyce, disponible gratuitamente en su página web.

Este post ha sido realizado por Pablo Rodríguez (@DonMostrenco) y es una colaboración de Naukas.com con la Cátedra de Cultura Científica de la UPV/EHU.